Absorbed lumped irradiance

Absorption of lumped irradiance can be calculated following two models, respectively Beer’s law (Monsi and Saeki, 1953) and de Pury et al. (1997).

Beer’s law

Monsi and Saeki (1953) were probably the first to use Beer-Lambert’s law in order to simulate irradiance transfer through crop canopies. Following this approach, leaves are assumed to form a continuous turbid medium that intercepts the incident irradiance \(I_{inc} \ [W \cdot m^{-2}_{ground}]\) and the ability of the canopy to transfer irradiance is represented by the so-called so-called extinction coefficient property \(k_{lumped} \ [m^2_{ground} \cdot m^{-2}_{leaf}]\).

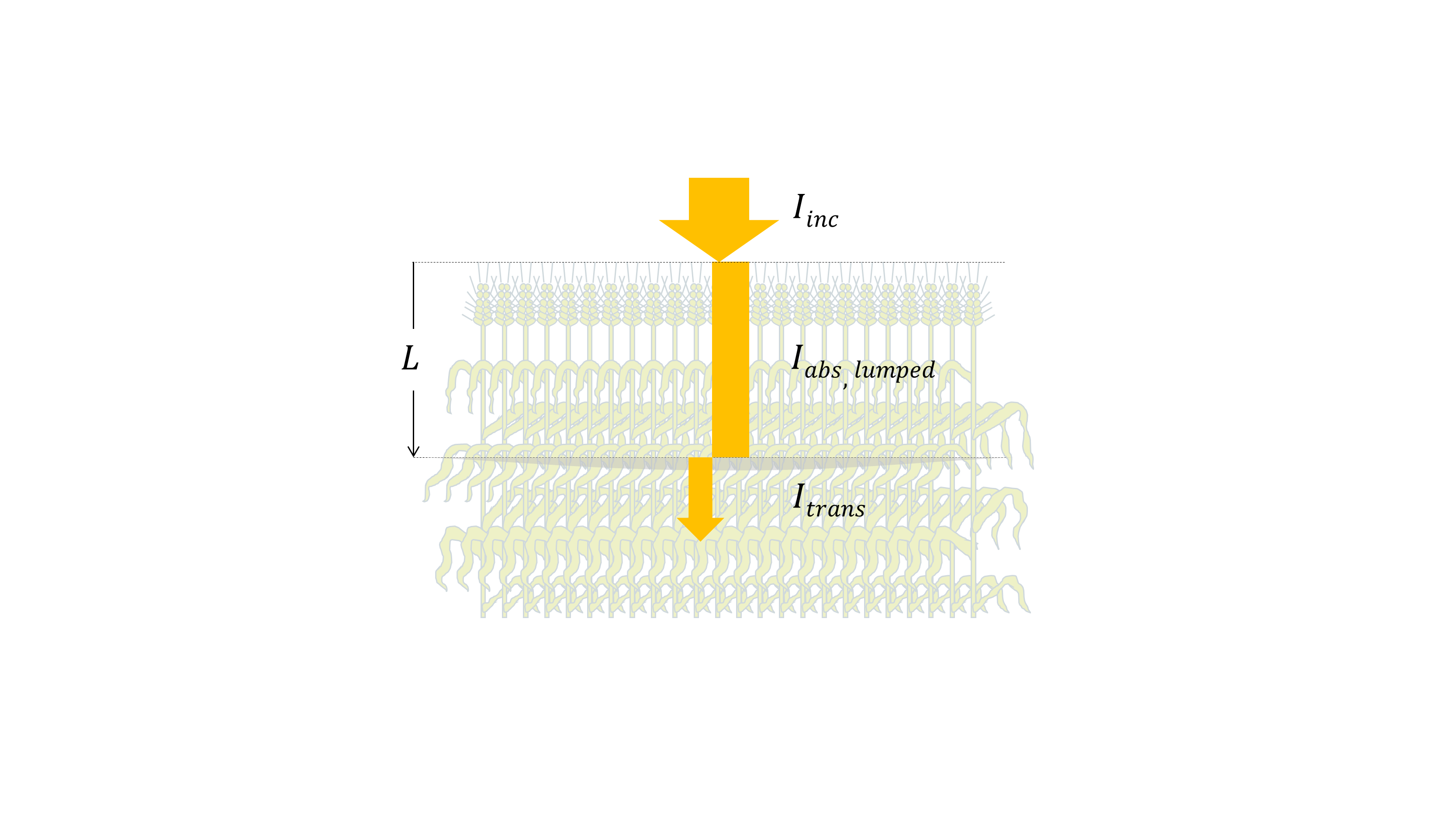
Fig. 5 Lumped irradiance absoption. \(L \ [m^2_{leaf} \cdot m^{-2}_{ground}]\) is downward-cumulative leaf area index, \(I_{inc} \ [W \cdot m^{-2}_{ground}]\) is the incident global irradiance, \(I_{trans} \ [W \cdot m^{-2}_{ground}]\) is the transmitted global irradiance below \(L\), \(I_{abs, \ lumped} \ [W \cdot m^{-2}_{ground}]\) is the absorbed lumped irradiance by leaves throughout \(L\).

Below a given depth \(L \ [m^2_{leaf} \cdot m^{-2}_{ground}]\) inside the canopy, the flux density of the transmitted irradiance \(I_{trans} \ [W \cdot m^{-2}_{ground}]\) is calculated as:

(1)\[I_{trans} = I_{inc} \cdot \exp \left( -k_{lumped} \cdot L \right)\]

Given a finite leaf layer of a thickness \(dL \ [m^2_{leaf} \cdot m^{-2}_{ground}]\) at depth \(L\) , the absorbed lumped irradiance \(d I_{abs} \ [W \cdot m^{-2}_{ground}]\) can be calculated as:

(2)\[\begin{split}\frac{d I_{abs, \ lumped}}{d L} =& - \frac{d I_{trans}}{d L} \\ =& k_{lumped} \cdot I_{inc} \cdot \exp(-k_{lumped} \cdot L)\end{split}\]

Layered canopies

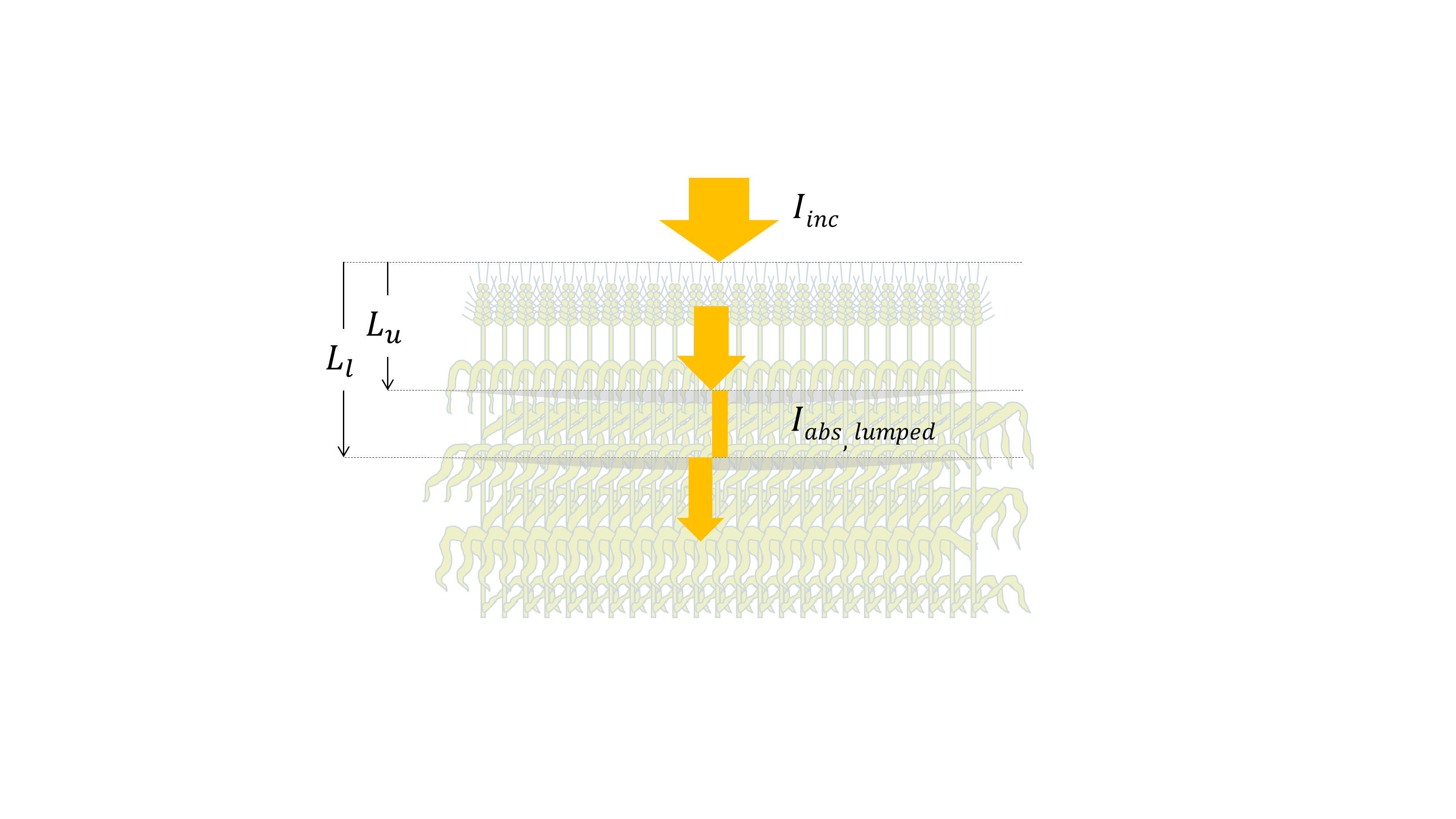
Fig. 6 Lumped irradiance absoption by a leaf layer spanning between upper \(L_u [m^2_{leaf} \cdot m^{-2}_{ground}]\) and lower \(L_l [m^2_{leaf} \cdot m^{-2}_{ground}]\) depths.

The rate of the absorbed irradiance of a leaf layer that spands between an upper depth \(L_u \ [m^2_{leaf} \cdot m^{-2}_{ground}]\) and a lower depth \(L_l \ [m^2_{leaf} \cdot m^{-2}_{ground}]\) (Fig. 6) is obtained from (2) as:

(3)\[I_{abs, \ lumped} = \int_{L_u}^{L_l} {k_{lumped} \cdot I_{inc} \cdot \exp(-k_{lumped} \cdot L) \ dL}\]

which yields:

(4)\[I_{abs, \ lumped} = I_{inc} \cdot \left[ \exp(-k_{lumped} \cdot L_u) - exp(-k_{lumped} \cdot L_l) \right]\]

Bigleaf canopies

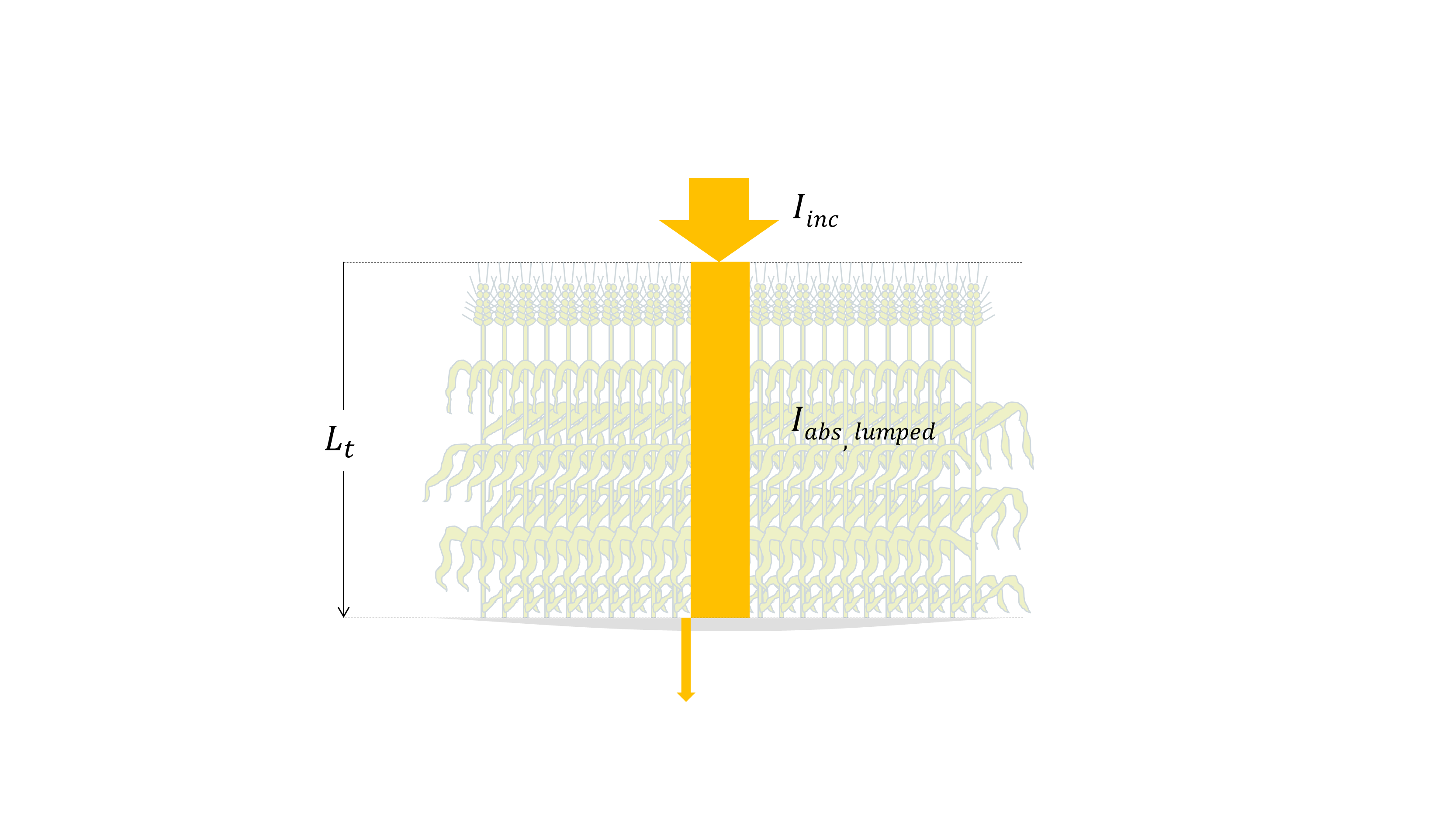
Fig. 7 Lumped irradiance absoption by a bigleaf canopy. \(L_t [m^2_{leaf} \cdot m^{-2}_{ground}]\) is the total leaf area index.

Irradiance absorption by a bigleaf canopy (Fig. 7) is simply derived from (4) by replacing \(L_u\) and \(L_l\) by 0 and the total leaf area index \(L_{t} \ [m^2_{leaf} \cdot m^{-2}_{ground}]\), respectively, which yields:

(5)\[I_{abs, \ lumped} = I_{inc} \cdot \left[1 - \exp(-k_{lumped} \cdot L_t) \right]\]

de Pury and Farquhar (1997)

This model is simplified from Goudriaan models (Goudriaan, 1977; 1988; 1994; 2016) by disregarding the scattering effect of leaves. de Pury and Farquhar (1997) calculated the absorbed lumped irradiance as the sum of absorbed direct and diffuse irradiance rates, respectively \(I_{abs, \ direct}\) and \(I_{abs, \ diffuse} \ [W \cdot m^{-2}_{ground}]\):

(6)\[I_{abs, \ lumped} = I_{abs, \ direct} + I_{abs, \ diffuse}\]

Layered canopies

On a ground area basis, the absorbed lumped irradiance by a leaf layer spanning between depths \(L_u\) and \(L_l \ [m^2_{leaf} \cdot m^{-2}_{ground}]\) writes:

(7)\[\begin{split}I_{abs, \ lumped} &= I_{inc, \ direct} \cdot (1 - \rho_{direct}) \cdot \left( \exp(-k_{direct} \cdot L_u) - \exp(-k_{direct} \cdot L_l) \right) \\ &+ I_{inc, \ diffuse} \cdot (1 - \rho_{diffuse}) \cdot \left( \exp(-k_{diffuse} \cdot L_u) - \exp(-k_{diffuse} \cdot L_l) \right)\end{split}\]

where \(I_{inc, \ direct} \ [W \cdot m^{-2}_{ground}]\) is the incident direct (beam) irradiance, \(I_{inc, \ diffuse} \ [W \cdot m^{-2}_{ground}]\) is the incident sky-diffused irradiance, \(\rho_{direct} \ [-]\) is canopy reflectance to direct irradiance, \(\rho_{diffuse} \ [-]\) is canopy reflectance to diffuse irradiance, \(k_{direct} \ [m^2_{ground} \cdot m^{-2}_{leaf}]\) is the extinction coefficient of the direct irradiance, and \(k_{diffuse} \ [m^2_{ground} \cdot m^{-2}_{leaf}]\) is the extinction coefficient of the diffuse irradiance. These variables are thoroughly described in Absorbed irradiance by sunlit and shaded leaf fractions.

Bigleaf canopies

For a bigleaf canopy, equation (7) become:

(8)\[\begin{split}I_{abs, \ lumped} &= I_{inc, \ direct} \cdot (1 - \rho_{direct}) \cdot \left( 1 - \exp(-k_{direct} \cdot L_t) \right) \\ &+ I_{inc, \ diffuse} \cdot (1 - \rho_{diffuse}) \cdot \left( 1 - \exp(-k_{diffuse} \cdot L_t) \right)\end{split}\]